Nov 27, · 三角形の内角 三角形の3つの内角の和 → 必ず180°になる 問題 xの角度は??簡単だね?3つの内角を全て足し算すると180°だから、 40°65°∠x=180° ∠x=75° ・・・(答え) 三角形の外角 赤色の角度のことを、ぜんぶ 「外角」 と呼ぶよ!Apr , 19 · 三角形に直線を引いて、二つの直角三角形となることがわかるのなら、どの角度にも三角比の値を定義して、問題はない。 正弦定理、余弦定理の求め方、三角形いろいろ「三角比の応用」 「微積分とはどのような方法か?」瞬間を切り取る小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
三角形 角度の求め方
三角形 角度の求め方-Jun 02, 18 · 上野竜生です。三角形の辺や角が3つわかれば基本的に残りの3つも計算できます。その求め方をすべてのパターン網羅して考えます。 暗黙の了解 三角形abcにおいて∠aや∠b,∠cを単にa,b,cとし,aは辺bcの長さ,bは辺Feb 19, 21 · この記事では、「三角形」の面積公式や角度・辺の長さ・重心の求め方などを紹介していきます。 また合同条件や、比の計算問題の解き方も詳しく解説していくので、ぜひマスターしてくださいね! 目次三角形とは?三角形の面積の公式




点oが三角形abcの外心であるときのaの角度の求め方を教えてください Clear
Aug 01, 19 · 三角形の外角の大きさ=となり合わない2つの内角の和 であることから x+60°=135° x=135°-60°=75°・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度三角形の「2辺の長さの比」が正弦の値になるのは直角三角形の場合だけで、それ以外の場合には sin A の値は「2辺の長さの比」にはなりません。 (右図イのような場合も含めて)一般に、角度 A の値によって sin A の値が決まり、これとは別に辺の長さが決められていると考えることが重要です。
三角形の面積は「 \(底辺×高さ÷2\) 」という公式から求まりますが、この公式以外にも色々な方法で三角形の面積を求めることができます。 このページでは、そんな三角形の面積の求め方をタイプ別に見ていきましょう。Dec 09, · 先生 (1)三角形の内角の和と外角の定理を利用して、三角形の角の大きさを求めましょう。 まず、内角と外角とは何か学んでいきましょう。 三角形の内角の和は、全ての 多角形 たかっけい の角度を求めるときの基礎です。 三角形の内角の和というのは,三角形の内側の角の大きさの和のことをいいます。 三角形の内角の和=180° 小学生女の子 正三角形の1つFeb 03, · 三角定規の角度 三角定規は2種類の直角三角形で90°が1つ入っています。 残りの2つの角度が分かるようにします。 その1 1つ目の三角定規は正方形を半分にした直角二等辺三角形で、90°以外の角度は2つとも45°です。
右図の方でしっかり四角形の4つの角が三角形を構成する角になっていることが分かると思います。 同じように、他の多角形でも線を引いて、内角の和を知ることが出来ます。 さて、四角形から八角形までの内角の和を求めてみましょう! 内角の和には規則Aug 09, 18 · あとは「三角形の内角の和は \(180°\) 」「直線は \(180°\)」を使うと \(∠BAT=∠ACB\) となり、接弦定理を証明できました。 円の接線が接点を通る直径と垂直になる理由Jun 02, 21 · 簡単な三角関数ですが、小数点以下と角度を求めるのに便利に使わせて頂きました。 ありがとうございました。 1402



直角三角形 底辺と角度 三角形の計算 計算サイト



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ
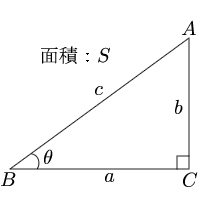
Mar 16, 21 · 三角比・三角関数を攻略するためには、sin・cos・tan(サイン・コサイン・タンジェント)の値を確実に求められるようになることが重要だ。また、有名角の三角比を自由自在に使えるようになることが特に重要なので、しっかりと学習してほしい。さらに、相互関係の公式を利用して、三角比をまずは、角度Bは簡単に求まります。三角形の内角の和は180度ですから、「C = 180 A B = 180 35 90 = 55」より、角Cの大きさは55度だと分かります。 aとbの求め方 次に、aとbを求めてみま三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
Apr 04, · 以上をまとめると三角方程式の解き方は「 単位円 を描き、 y=aの直線 を加えて、 三角形の比 を求めて角度を求め、 範囲を確認 して当てはまるもののみ答える」となります。Feb 19, 21 · 基本的に、三角関数の角度は 半径 の「単位円」 を利用して求めることができます。 単位円 周分の角度は、度数なら 、ラジアンなら です。正多角形の内角・外角の求め方を解説! 星形の角度の求め方を解説!←今回の記事 ブーメラン型の角度の求め方! ちょうちょ型の角度の求め方を解説! 合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法!



表計算ソフトを使って 底辺 と 高さ から 角度 を求める




小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ
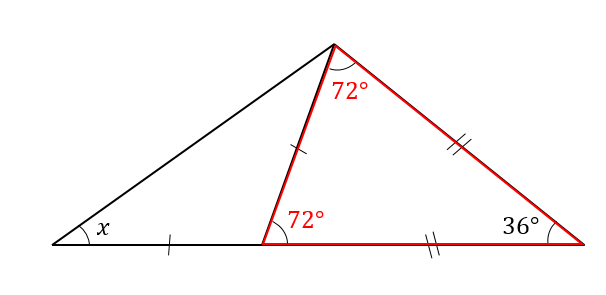
右の図で三角形FPDに着目すると、三角形の内角の和は180°だから、 180°-(70°+90°)=° で、角FPDは°です。 さらにPに着目して、直線の角は180°であることより$15^\circ$ の三角比の値は覚えなくてもよいが、$15^\circ$ を含む直角三角形から導けるようにしておこう。 これらの角以外にも、$18^\circ$、$36^\circ$、$72^\circ$、$144^\circ$ などの角も、特殊な三角形を考えることによって三角比を 求めることができる。Apr 28, · まずbの角度から求めていきます。向かい合った角、つまり対頂角は等しいので、b=30° 次にaの角度を求めます。直線の角の大きさは180°です。そのためaの角度は、180°30°=150° cの角度は対頂角よりaと等しいので、c=150° よって、 答え a=150°、b=30°、c=150°




三角形の内角の和を帰納的 演繹的に求める方法 算数を究める



直角三角形の解法 1
Aug 26, 18 · 三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。三角形の形状問題 三角形の証明問題 内接円の半径 正弦・余弦・面積 (センター問題) 三角比のセンター試験問題 → スg スム版は別包ソス ス ス スO スモ ソス スp スs ス ス スt ス ス ス@ ス ス ス ス阯晢ソス@ ス ス スQ ス ス ス ス スQ ス ス スQ 2 ス ス直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「=11*SIN(RADIANS (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン(arcsin、逆正弦)、アークコサイン




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
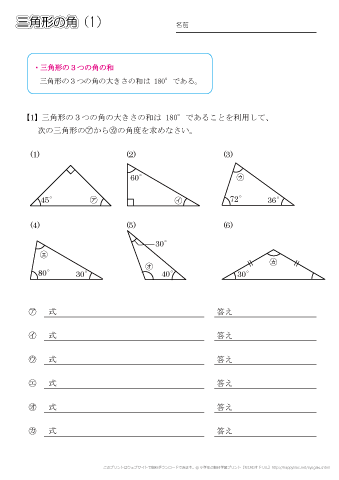



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
3年算数三角形教え方のポイント ① 三角形の仲間分け ② 二等辺三角形・正三角形の理解 ③ コンパス・定規を使っての二等辺三角形・正三角形のかき方 2年生の三角形の勉強 は 直角のところをみていました が、3年の三角形の勉強は、 辺の長さを特にみつまり、角度をもとに辺の比を求めているわけです。 それに対し、逆三角関数は「底辺と対辺の比が なら、その辺に対する直角三角形の角は30°になる」ということを表しています。 逆三角関数の考え方 図1を使って、逆三角関数を考えてみましょう。解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。




数学 中2 53 角度チャレンジ Lv 1 Youtube




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
Oct 27, 09 · 数学はまったくの初心者です。AOの距離をaOBの距離をbとしたときのθの求め方をなるべく簡潔に教えてください。当方、数学はまったくの初心者ですので、わかりやすい解説などもあるとありがたいです。a≠bということは、ご質問の図のようにMar 17, 09 · 直角三角形の角度θの求め方について質問です。 ※三角形の内角は30°60°90°です。 斜辺の長さがわからない時のθの求め方として、「tanθ=底辺a×高さb」の公式を使うと思うのですが、この公式ですとθが30°では なく33°になってしまいます。Oct 30, 16 · まず覚えておいておくべき直角三角形の辺の比は、 12√3 だよ。 この辺の比になる直角三角形の角度は、 30° 60° 90° になってるんだ。 例えば、次の直角三角形ABCがあったとして、辺BCの長さが2cmだったとしよう。



内接円 内心
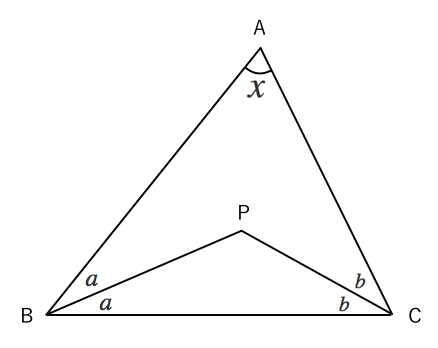



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に
Mar 08, 05 · すると角aは三角形イ、ウ、エの外角になっています。(旗が逆さになっています) 三角形の内角と外角の関係から = + 角A = 30°+ 90° = 1° と計算できます。Jan 13, 18 · (考え方)アの図形は、底辺が6cm、高さが3cmの三角形で、面積が9㎠です。高さが3cmになるのは、30度・60度の直角三角形の性質によるものです。イとウの図形はそれぞれ中心角が30度と90度のおうぎ形で、面積は合わせて3768㎠です。




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典




底辺と角度から 高さを求める ある高さの木から 10m離れて 木のてっ Okwave



普通の電卓で計算できる直角三角形の近似計算
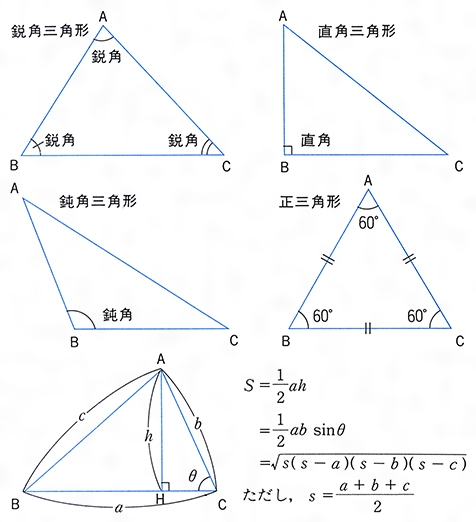



三角形とは コトバンク




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo




外角の求め方 外角の和を使って多角形の角度を求める問題 中学や高校の数学の計算問題




直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage




小5 算数 小5 31 三角形の角 Youtube
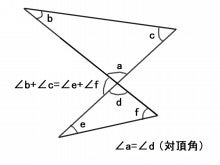



角度の求め方 数学が嫌いなんです



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



直角三角形の解法 1




角度の計算 裏技まとめ 教遊者




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット




点oが三角形abcの外心であるときのaの角度の求め方を教えてください Clear



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター




角度の求め方 算数の教え上手 学びの場 Com




三角形の内角の和を帰納的 演繹的に求める方法 算数を究める




角度の問題まとめ 無料で使える中学学習プリント




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ
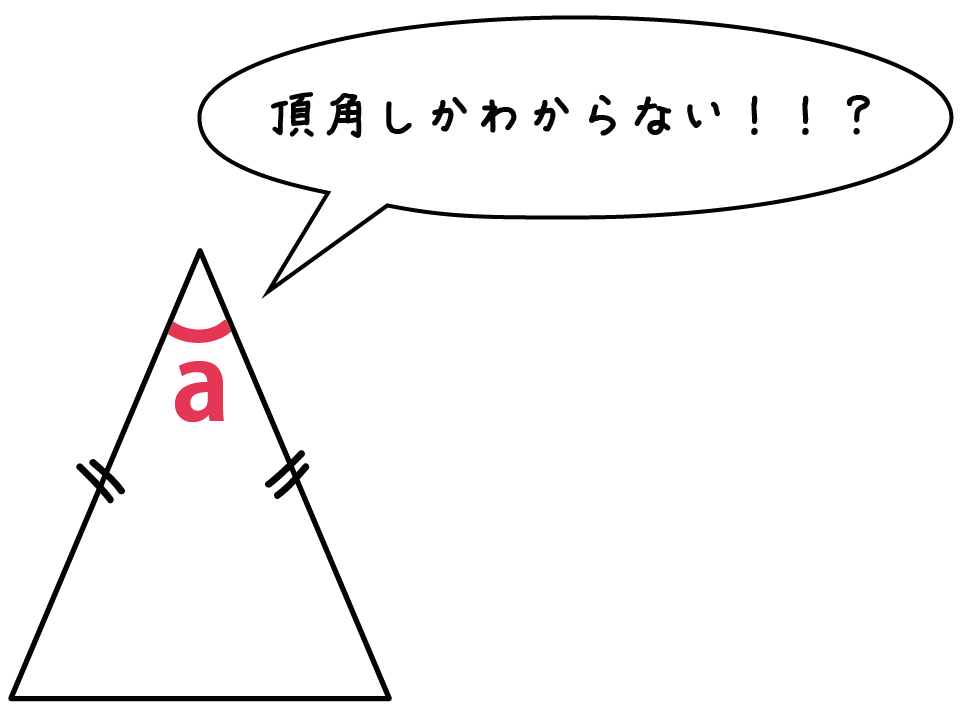



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく
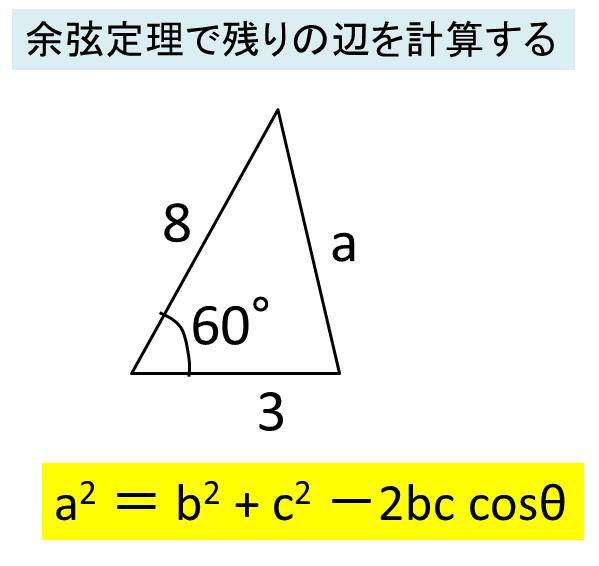



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める
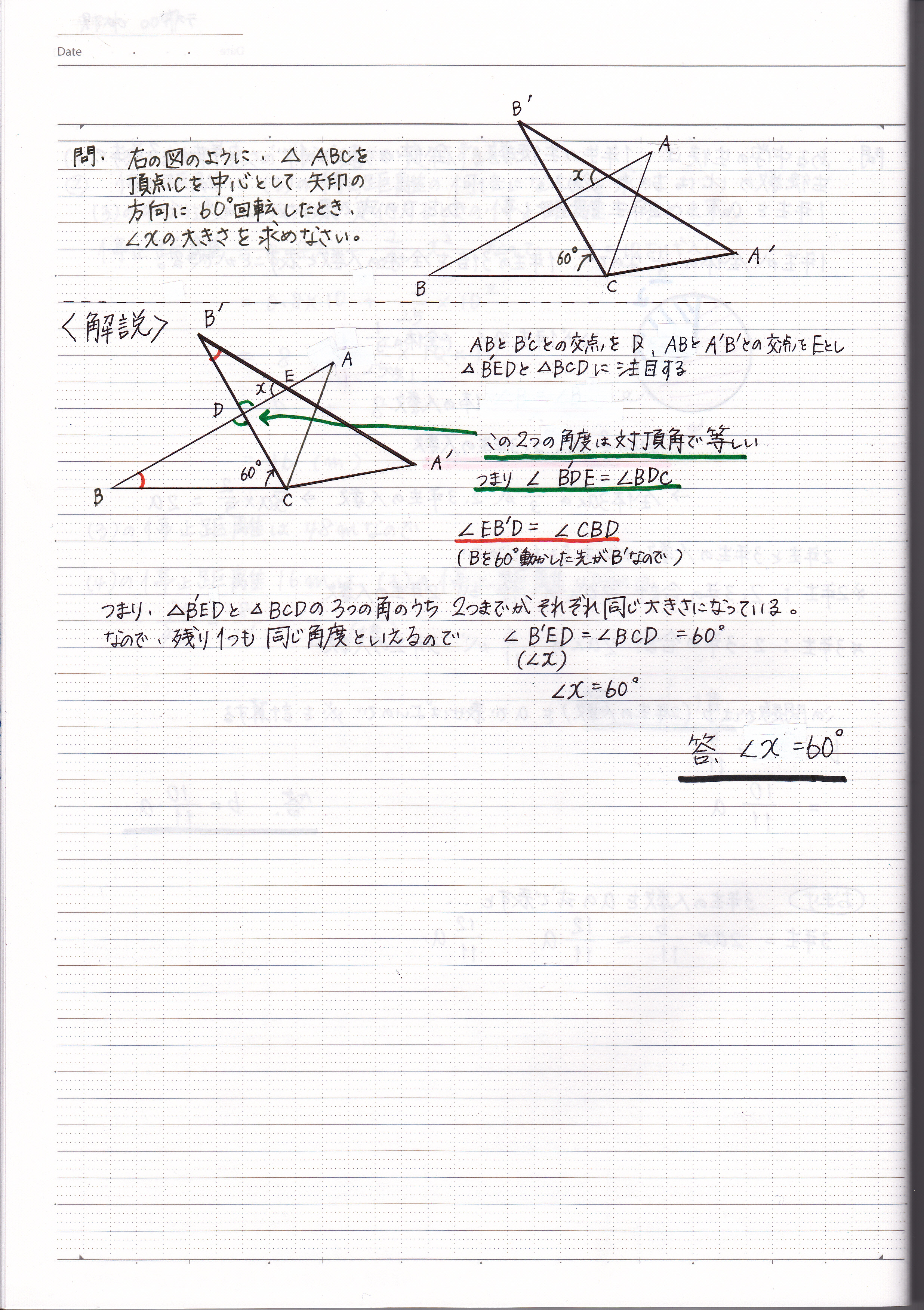



回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく
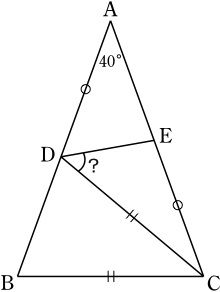



二等辺三角形の頂角を求める問題の 逆 の問題 東大合格コム



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
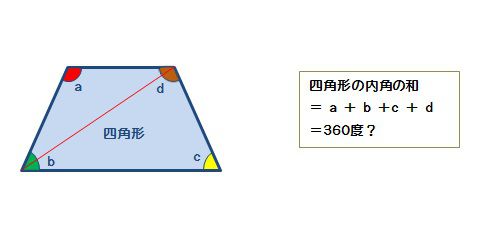



四角形の内角の和 算数の公式覚えてますか




小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
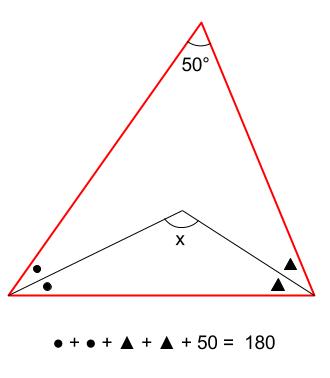



中学数学 求角と方程式 中学数学の無料オンライン学習サイトchu Su



三角形の角度を求める 思考力を鍛える数学
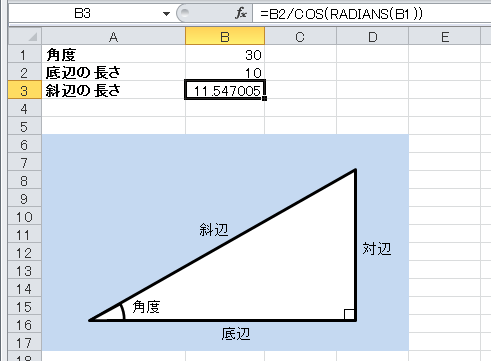



角度からコサインを計算するには Cos Radiansの解説 エクセル関数リファレンス




内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学



円と三角形 角度 中学から数学だいすき
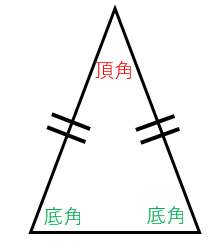



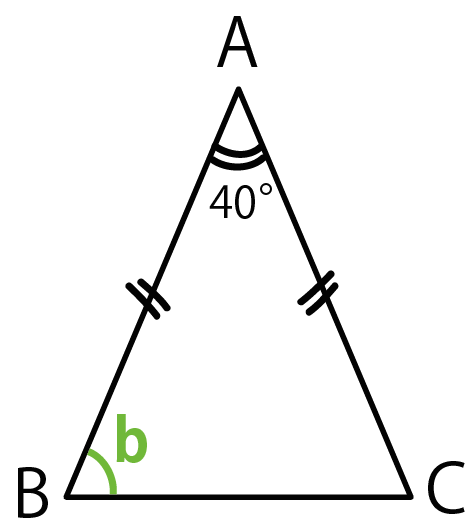
二等辺三角形の角度の求め方と例題 具体例で学ぶ数学




あ かまでの角度を求めてください 急いでます 教えてください Clear




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



三角関数 1 Cg 数学 06aa
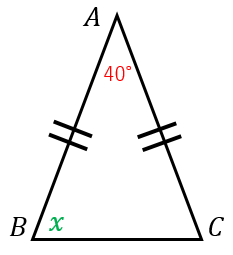



二等辺三角形の角度の求め方と例題 具体例で学ぶ数学




中2 数学 4 2 三角形の角度の利用 Youtube



二等辺三角形とは 定義や定理 角度 辺の長さ 面積の求め方 受験辞典
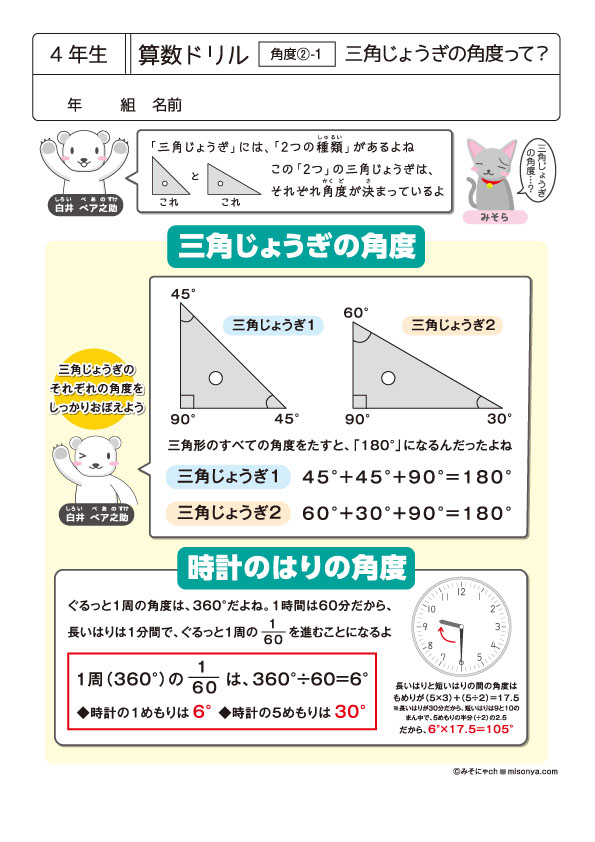



無料の学習プリント 小学4年生の算数ドリル 角度2 三角定規と時計の針 みそにゃch




三角形の角度を求める問題 小学生 中学生の勉強
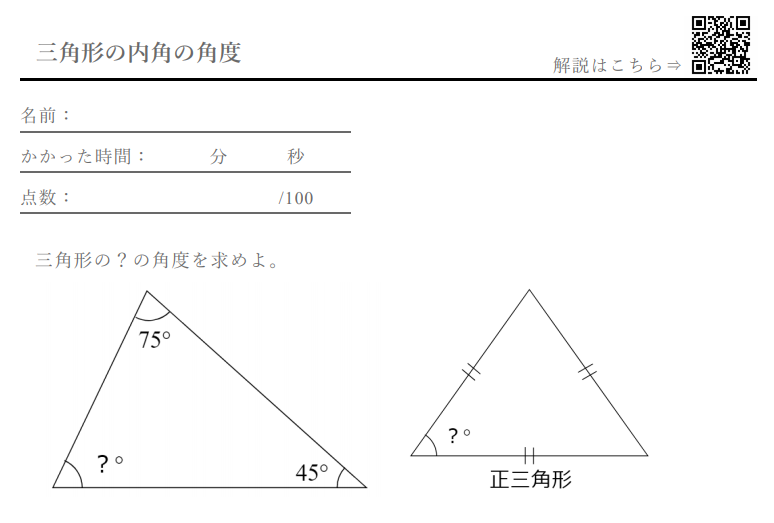



三角形 の内角の角度 計算ドリル 問題集 数学fun



添付した図のような台形の xの角度を求めようと思っています 参 Yahoo 知恵袋
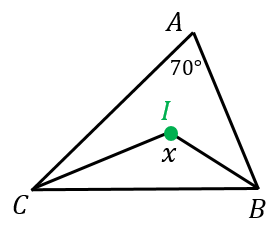



三角形の内心の証明と頻出例題2問 具体例で学ぶ数学



中学二年 数学 三角形の角度の求め方 中の上編 Youtube
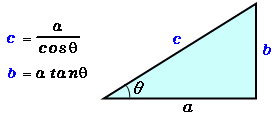



角度と底辺から斜辺と高さを計算 高精度計算サイト




正三角形や二等辺三角形の内角 Youtube



角度の求め方 算数の教え上手 学びの場 Com




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット




角度の求め方 算数の教え上手 学びの場 Com




余弦定理で角度を求める方法 数学の星



Q Tbn And9gcsdwwj5sbz Wtzefjn4b8ztn1e Cykqzeuj 9xadmx7v98lf7vu Usqp Cau




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算




円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi
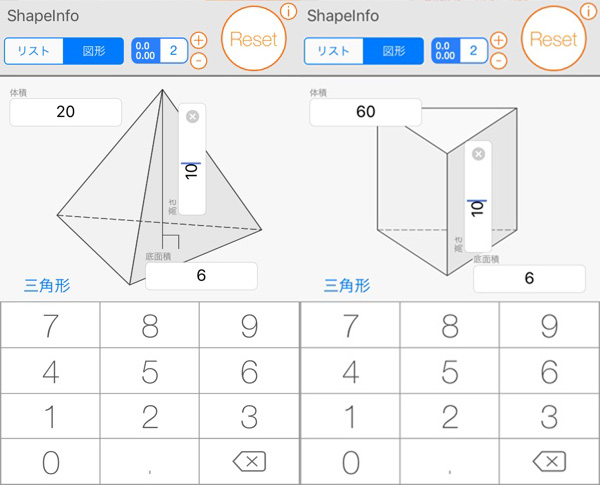



三角形や球も 様々な図形の面積や角度がすぐに分かる 図形電卓 が超便利 Isuta イスタ 私の 好き にウソをつかない




タンジェントとは何か 中学生でも分かる三角関数の基礎
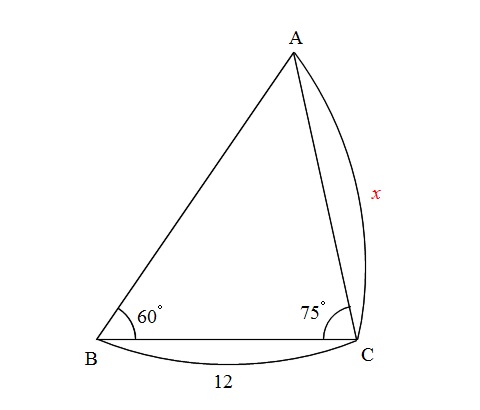



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない




二等辺三角形を使う角度計算です 一応解けたのですがもっと簡単な式があると思うので教え Clear



円と三角形 角度 中学から数学だいすき




三角形の角度を求める問題 小学生 中学生の勉強
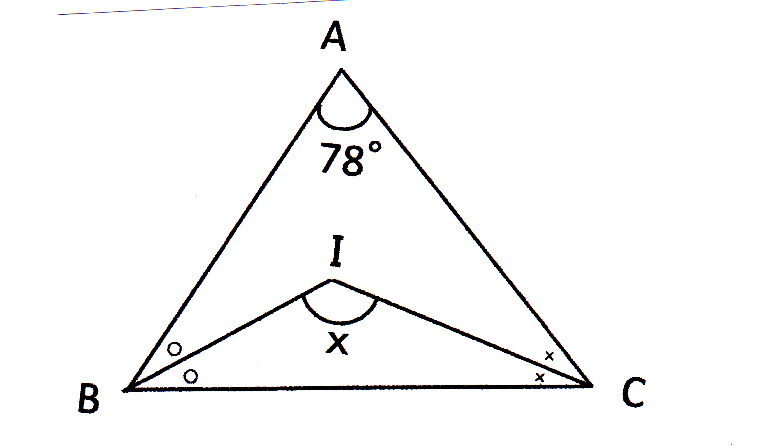



三角形内の角度を求める問題 現役塾講師のわかりやすい中学数学の解き方




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




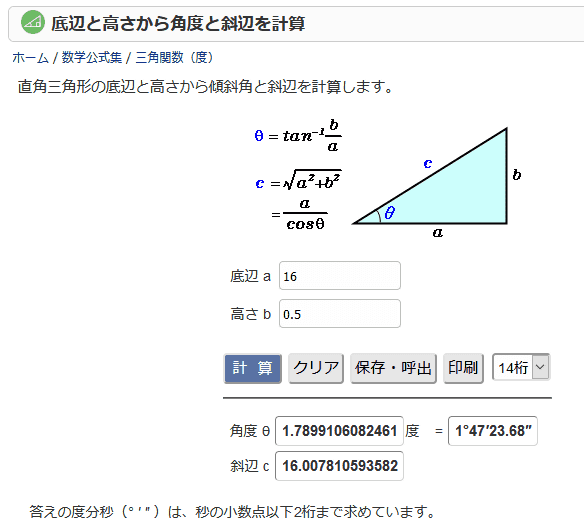
底辺と高さから角度と斜辺を計算 高精度計算サイト



三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す
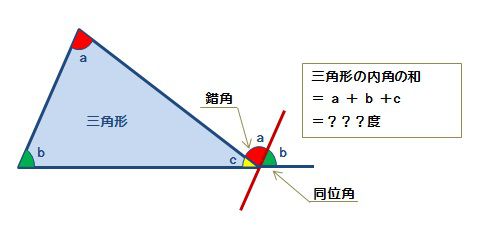



三角形の内角の和 算数の公式覚えてますか
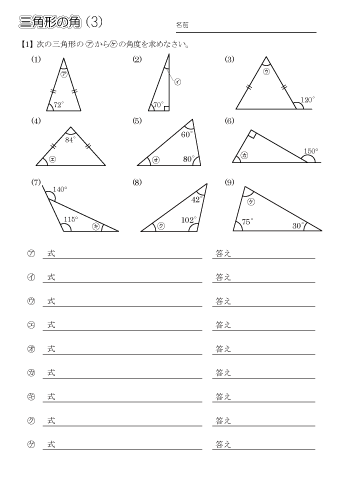



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
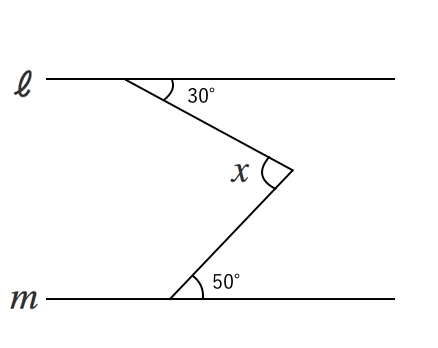



図形の調べ方 角度を求める問題 苦手な数学を簡単に




三角形の3辺から角度を計算 高精度計算サイト



1
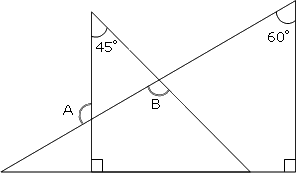



角度の求め方 算数の教え上手 学びの場 Com




中高生必読 知らないとヤバい二等辺三角形の知識 定義 角度 面積 高校生向け受験応援メディア 受験のミカタ



1



1
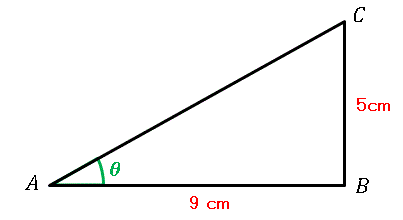



Excel で直角三角形の斜辺と底辺に挟まれた角度を求めます




中2数学 ブーメラン型角度の求め方を解説 数スタ




三角形の辺から角度を計算 製品設計知識
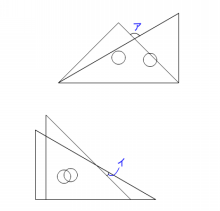



重なり合う三角定規を使った角度の計算問題 小4 小5の算数 きいとこ




高校数学 三角形の辺と角の関係 映像授業のtry It トライイット




ベスト三角形 角度 求め方 Tan 最高のぬりえ




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ




1 Descubre Como Resolverlo En Qanda



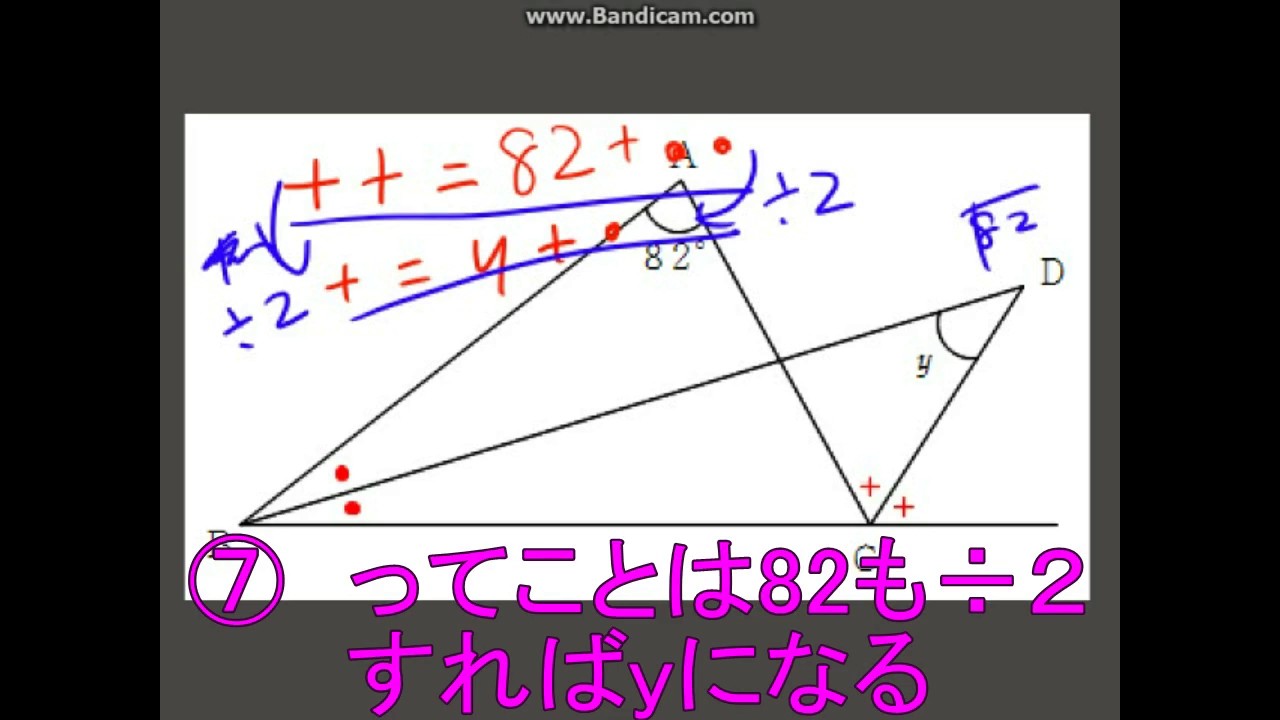
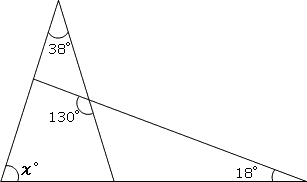
ラングレーの問題 整角四角形




二等辺三角形の角を求める Youtube




二等辺三角形の定義 角度の性質を使った証明問題などを解説 遊ぶ数学



二等辺三角形の底辺は 1分でわかる意味 長さの計算 角度 高さ 三平方の定理との関係




多角形の内角の和の公式と外角の和を利用した角度の求め方



0 件のコメント:
コメントを投稿